前端游戏巨制! CSS 居然可以做 3D 游戏了
↓推荐关注↓
前言
偶然接触到CSS的3D属性, 就萌生了一种做3D游戏的想法.
了解过css3D属性的同学应该都了解过perspective、perspective-origin、transform-style: preserve-3d这个三个属性值, 它们构成了CSS的3d世界.
同时, 还有transform属性来对3D的节点进行平移、缩放、旋转以及拉伸.
属性值很简单, 在我们平时的web开发中也很少用到.
那用这些CSS3D属性可以做3D游戏吗?
当然是可以的.
即使只有沙盒, 也有我的世界这种神作.
今天我就来带大家玩一个从未有过的全新3D体验.
废话不多说, 我们先来看下效果:

我们要完成这个迷宫大作战,需要完成以下步骤:
创建一个3D世界 写一个3D相机的功能 创建一座3D迷宫 创建一个可以自由运动的玩家 在迷宫中找出一条最短路径提示
我们先来看下一些前置知识.
做一款CSS3D游戏需要的知识和概念
CSS3D坐标系
在css3D中, 首先要明确一个概念, 3D坐标系.
使用左手坐标系, 伸出我们的左手, 大拇指和食指成L状, 其他手指与食指垂直, 如图:
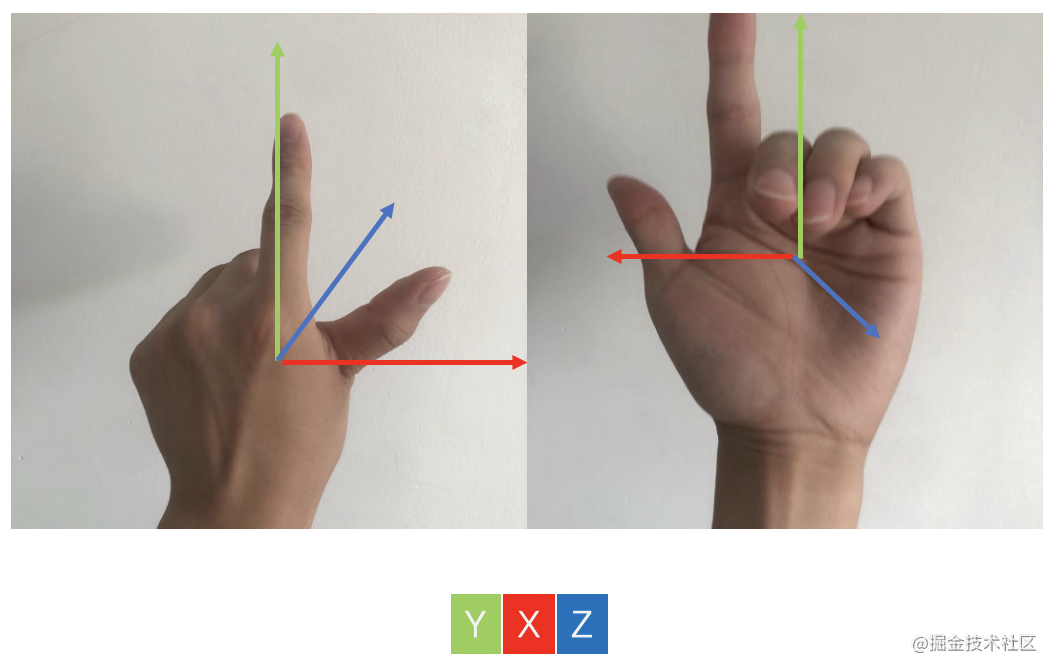
大拇指为X轴, 食指为Y轴, 其他手指为Z轴.
这个就是CSS3D中的坐标系.
透视属性
perspective为css中的透视属性.
这个属性是什么意思呢, 可以把我们的眼睛看作观察点, 眼睛到目标物体的距离就是视距, 也就是这里说的透视属性.
大家都知道, 「透视」+「2D」= 「3D」.
perspective: 1200px;
-webkit-perspective: 1200px;
3D相机
在3D游戏开发中, 会有相机的概念, 即是人眼所见皆是相机所见.
在游戏中场景的移动, 大部分都是移动相机.
例如赛车游戏中, 相机就是跟随车子移动, 所以我们才能看到一路的风景.
在这里, 我们会使用CSS去实现一个伪3d相机.
变换属性
在CSS3D中我们对3D盒子做平移、旋转、拉伸、缩放使用transform属性.
translateX 平移X轴 translateY 平移Y轴 translateZ 平移Z轴 rotateX 旋转X轴 rotateY 旋转Y轴 rotateZ 旋转Z轴 rotate3d(x,y,z,deg) 旋转X、Y、Z轴多少度
注意:
这里「先平移再旋转」和「先旋转再平移」是不一样的
旋转的角度都是角度值.
矩阵变换
我们完成游戏的过程中会用到矩阵变换.
在js中, 获取某个节点的transform属性, 会得到一个矩阵, 这里我打印一下, 他就是长这个样子:
var _ground = document.getElementsByClassName("ground")[0];
var bg_style = document.defaultView.getComputedStyle(_ground, null).transform;
console.log("矩阵变换---->>>",bg_style)
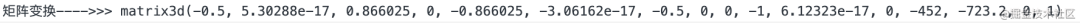
那么我们如何使用矩阵去操作transform呢?
在线性变换中, 我们都会去使用矩阵的相乘.
CSS3D中使用4*4的矩阵进行3D变换.
下面的矩阵我均用二维数组表示.
例如matrix3d(1,0,0,0,0,1,0,0,0,0,0,1,0,0,0,0,1)可以用二维数组表示:
[
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
平移即使使用原来状态的矩阵和以下矩阵相乘, dx, dy, dz分别是移动的方向x, y, z.
[
[1, 0, 0, dx],
[0, 1, 0, dy],
[0, 0, 1, dz],
[0, 0, 0, 1]
]
绕X轴旋转𝞱, 即是与以下矩阵相乘.
[
[1, 0, 0, 0],
[0, cos𝞱, sin𝞱, 0],
[0, -sin𝞱, cos𝞱, 0],
[0, 0, 0, 1]
]
绕Y轴旋转𝞱, 即是与以下矩阵相乘.
[
[cos𝞱, 0, -sin𝞱, 0],
[0, 1, 0, 0],
[sin𝞱, 0, cos𝞱, 0],
[0, 0, 0, 1]
]
绕Z轴旋转𝞱, 即是与以下矩阵相乘.
[
[cos𝞱, sin𝞱, 0, 0],
[-sin𝞱, cos𝞱, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]
]
具体的矩阵的其他知识这里讲了, 大家有兴趣可以自行下去学习.
我们这里只需要很简单的旋转应用.
开始创建一个3D世界
我们先来创建UI界面.
相机div 地平线div 棋盘div 玩家div(这里是一个正方体)
注意
正方体先旋转在平移, 这种方法应该是最简单的.
一个平面绕X轴、Y轴旋转180度、±90度, 都只需要平移Z轴.
这里大家试过就明白了.
我们先来看下html部分:
<div class="camera">
<div class="ground">
<div class="box">
<div class="box-con">
<div class="wall">zdiv>
<div class="wall">zdiv>
<div class="wall">ydiv>
<div class="wall">ydiv>
<div class="wall">xdiv>
<div class="wall">xdiv>
<div class="linex">div>
<div class="liney">div>
<div class="linez">div>
div>
<div class="pan">div>
div>
div>
div>
很简单的布局, 其中linex、liney、linez是我画的坐标轴辅助线.
红线为X轴, 绿线为Y轴, 蓝线为Z轴. 接着我们来看下正方体的主要CSS代码.
...
.box-con{
width: 50px;
height: 50px;
transform-style: preserve-3d;
transform-origin: 50% 50%;
transform: translateZ(25px) ;
transition: all 2s cubic-bezier(0.075, 0.82, 0.165, 1);
}
.wall{
width: 100%;
height: 100%;
border: 1px solid #fdd894;
background-color: #fb7922;
}
.wall:nth-child(1) {
transform: translateZ(25px);
}
.wall:nth-child(2) {
transform: rotateX(180deg) translateZ(25px);
}
.wall:nth-child(3) {
transform: rotateX(90deg) translateZ(25px);
}
.wall:nth-child(4) {
transform: rotateX(-90deg) translateZ(25px);
}
.wall:nth-child(5) {
transform: rotateY(90deg) translateZ(25px);
}
.wall:nth-child(6) {
transform: rotateY(-90deg) translateZ(25px);
}
粘贴一大堆CSS代码显得很蠢.
其他CSS这里就不粘贴了, 有兴趣的同学可以直接下载源码查看. 界面搭建完成如图所示:

接下来就是重头戏了, 我们去写js代码来继续完成我们的游戏.
完成一个3D相机功能
相机在3D开发中必不可少, 使用相机功能不仅能查看3D世界模型, 同时也能实现很多实时的炫酷功能.
一个3d相机需要哪些功能?
最简单的, 上下左右能够360度无死角观察地图.同时需要拉近拉远视距.
通过鼠标交互
鼠标左右移动可以旋转查看地图; 鼠标上下移动可以观察上下地图; 鼠标滚轮可以拉近拉远视距.
✅ 1. 监听鼠标事件
首先, 我们需要通过监听鼠标事件来记录鼠标位置, 从而判断相机上下左右查看.
/** 鼠标上次位置 */
var lastX = 0, lastY = 0;
/** 控制一次滑动 */
var isDown = false;
/** 监听鼠标按下 */
document.addEventListener("mousedown", (e) => {
lastX = e.clientX;
lastY = e.clientY;
isDown = true;
});
/** 监听鼠标移动 */
document.addEventListener("mousemove", (e) => {
if (!isDown) return;
let _offsetX = e.clientX - lastX;
let _offsetY = e.clientY - lastY;
lastX = e.clientX;
lastY = e.clientY;
//判断方向
var dirH = 1, dirV = 1;
if (_offsetX < 0) {
dirH = -1;
}
if (_offsetY > 0) {
dirV = -1;
}
});
document.addEventListener("mouseup", (e) => {
isDown = false;
});
✅ 2. 判断相机上下左右
使用perspective-origin来设置相机的上下视线.
使用transform来旋转Z轴查看左右方向上的360度.
/** 监听鼠标移动 */
document.addEventListener("mousemove", (e) => {
if (!isDown) return;
let _offsetX = e.clientX - lastX;
let _offsetY = e.clientY - lastY;
lastX = e.clientX;
lastY = e.clientY;
var bg_style = document.defaultView.getComputedStyle(_ground, null).transform;
var camera_style = document.defaultView.getComputedStyle(_camera, null).perspectiveOrigin;
var matrix4 = new Matrix4();
var _cy = +camera_style.split(' ')[1].split('px')[0];
var str = bg_style.split("matrix3d(")[1].split(")")[0].split(",");
var oldMartrix4 = str.map((item) => +item);
var dirH = 1, dirV = 1;
if (_offsetX < 0) {
dirH = -1;
}
if (_offsetY > 0) {
dirV = -1;
}
//每次移动旋转角度
var angleZ = 2 * dirH;
var newMartri4 = matrix4.set(Math.cos(angleZ * Math.PI / 180), -Math.sin(angleZ * Math.PI / 180), 0, 0, Math.sin(angleZ * Math.PI / 180), Math.cos(angleZ * Math.PI / 180), 0, 0, 0, 0, 1, 0, 0, 0, 0, 1);
var new_mar = null;
if (Math.abs(_offsetX) > Math.abs(_offsetY)) {
new_mar = matrix4.multiplyMatrices(oldMartrix4, newMartri4);
} else {
_camera.style.perspectiveOrigin = `500px ${_cy + 10 * dirV}px`;
}
new_mar && (_ground.style.transform = `matrix3d(${new_mar.join(',')})`);
});
这里使用了矩阵的方法来旋转Z轴, 矩阵类Matrix4是我临时写的一个方法类, 就俩方法, 一个设置二维数组matrix4.set, 一个矩阵相乘matrix4.multiplyMatrices.
文末的源码地址中有, 这里就不再赘述了.
✅ 3. 监听滚轮拉近拉远距离
这里就是根据perspective来设置视距.
//监听滚轮
document.addEventListener('mousewheel', (e) => {
var per = document.defaultView.getComputedStyle(_camera, null).perspective;
let newper = (+per.split("px")[0] + Math.floor(e.deltaY / 10)) + "px";
_camera.style.perspective = newper
}, false);
注意:
perspective-origin属性只有X、Y两个值, 做不到和u3D一样的相机.
我这里取巧使用了对地平线的旋转, 从而达到一样的效果.
滚轮拉近拉远视距有点别扭, 和3D引擎区别还是很大.
完成之后可以看到如下的场景, 已经可以随时观察我们的地图了.

这样子, 一个3D相机就完成, 大家有兴趣的可以自己下去写一下, 还是很有意思的.
绘制迷宫棋盘
绘制格子地图最简单了, 我这里使用一个15*15的数组.
「0」代表可以通过的路, 「1」代表障碍物.
var grid = [
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0,
0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0,
1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1,
0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1,
0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0,
0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0,
1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0,
1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0,
0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1,
0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0,
1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0
];
然后我们去遍历这个数组, 得到地图.
写一个方法去创建地图格子, 同时返回格子数组和节点数组.
这里的block是在html中创建的一个预制体, 他是一个正方体.
然后通过克隆节点的方式添加进棋盘中.
/** 棋盘 */
function pan() {
const con = document.getElementsByClassName("pan")[0];
const block = document.getElementsByClassName("block")[0];
let elArr = [];
grid.forEach((item, index) => {
let r = Math.floor(index / 15);
let c = index % 15;
const gezi = document.createElement("div");
gezi.classList = "pan-item"
// gezi.innerHTML = `${r},${c}`
con.appendChild(gezi);
var newBlock = block.cloneNode(true);
//障碍物
if (item == 1) {
gezi.appendChild(newBlock);
blockArr.push(c + "-" + r);
}
elArr.push(gezi);
});
const panArr = arrTrans(15, grid);
return { elArr, panArr };
}
const panData = pan();
可以看到, 我们的界面已经变成了这样.
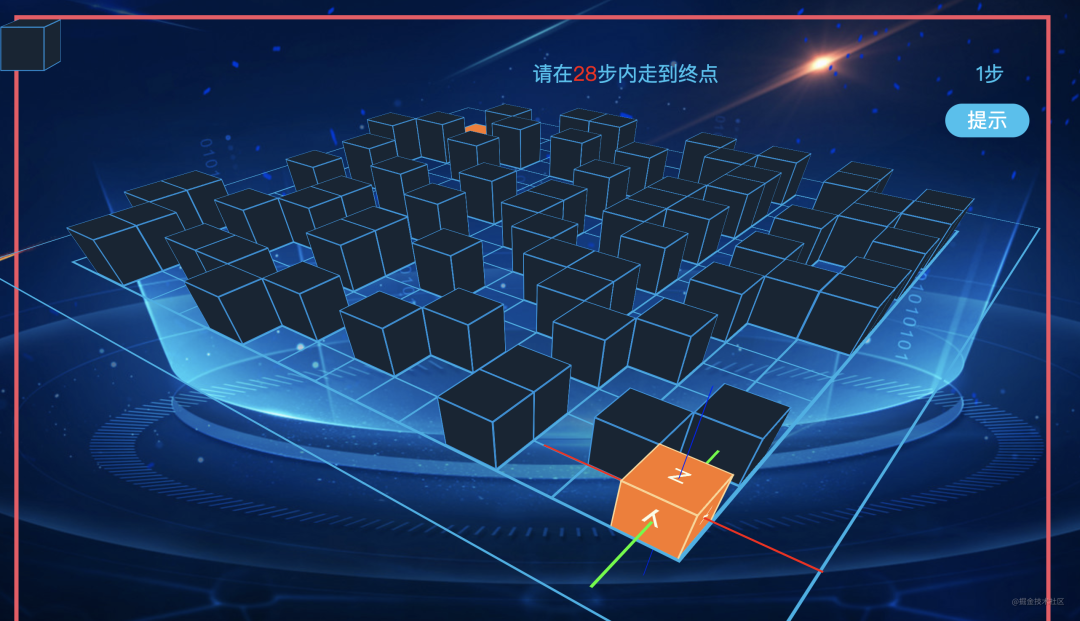
接下来, 我们需要去控制玩家移动了.
控制玩家移动
通过上下左右w s a d键来控制玩家移动.
使用transform来移动和旋转玩家盒子.
✅ 监听键盘事件
通过监听键盘事件onkeydown来判断key值的上下左右.
document.onkeydown = function (e) {
/** 移动物体 */
move(e.key);
}
✅ 进行位移
在位移中, 使用translate来平移, Z轴始终正对我们的相机, 所以我们只需要移动X轴和Y轴.
声明一个变量记录当前位置.
同时需要记录上次变换的transform的值, 这里我们就不继续矩阵变换了.
/** 当前位置 */
var position = { x: 0, y: 0 };
/** 记录上次变换值 */
var lastTransform = {
translateX: '0px',
translateY: '0px',
translateZ: '25px',
rotateX: '0deg',
rotateY: '0deg',
rotateZ: '0deg'
};
每一个格子都可以看成是二维数组的下标构成, 每次我们移动一个格子的距离.
switch (key) {
case 'w':
position.y++;
lastTransform.translateY = position.y * 50 + 'px';
break;
case 's':
position.y--;
lastTransform.translateY = position.y * 50 + 'px';
break;
case 'a':
position.x++;
lastTransform.translateX = position.x * 50 + 'px';
break;
case 'd':
position.x--;
lastTransform.translateX = position.x * 50 + 'px';
break;
}
//赋值样式
for (let item in lastTransform) {
strTransfrom += item + '(' + lastTransform[item] + ') ';
}
target.style.transform = strTransfrom;
到这里, 我们的玩家盒子已经可以移动了.
注意
在css3D中的平移可以看成是世界坐标.
所以我们只需要关心X、Y轴. 而不需要去移动Z轴. 即使我们进行了旋转.
✅ 在移动的过程中进行旋转
在CSS3D中, 3D旋转和其他3D引擎中不一样, 一般的诸如u3D、threejs中, 在每次旋转完成之后都会重新校对成世界坐标, 相对来说 就很好计算绕什么轴旋转多少度.
然而, 笔者也低估了CSS3D的旋转.
我以为上下左右滚动一个正方体很简单. 事实并非如此.
CSS3D的旋转涉及到四元数和万向锁.
比如我们旋转我们的玩家盒子. 如图所示:
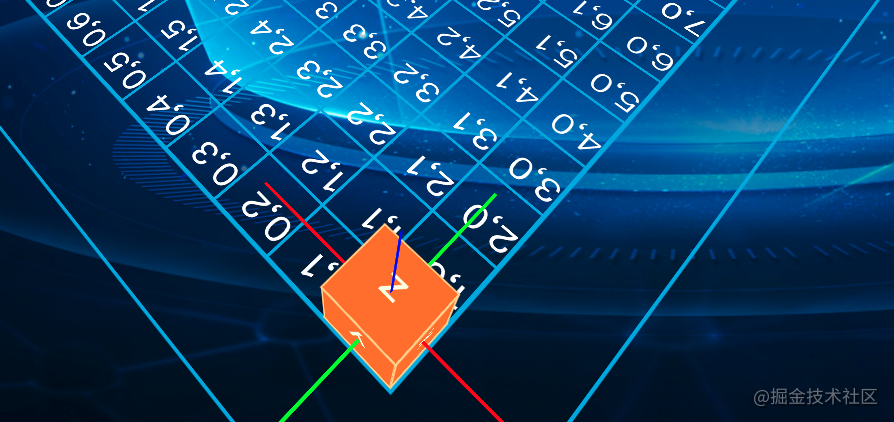 首先, 第一个格子(0,0)向上绕X轴旋转90度, 就可以到达(1.0); 向左绕Y轴旋转90度, 可以到达(0,1); 那我们是不是就可以得到规律如下:
首先, 第一个格子(0,0)向上绕X轴旋转90度, 就可以到达(1.0); 向左绕Y轴旋转90度, 可以到达(0,1); 那我们是不是就可以得到规律如下:
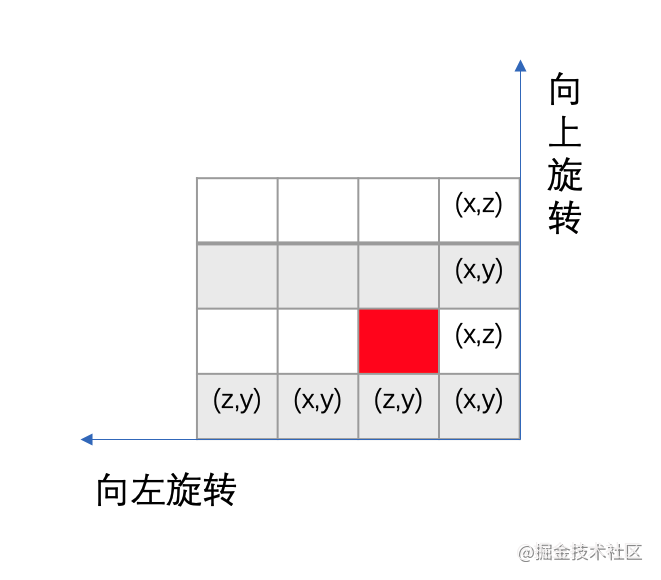
如图中所示, 单纯的向上下, 向左右绕轴旋转没有问题, 但是要旋转到红色的格子, 两种不同走法, 到红色的格子之后旋转就会出现两种可能. 从而导致旋转出错.
同时这个规律虽然难寻, 但是可以写出来, 最重要的是, 按照这个规律来旋转CSS3D中的盒子, 是不对的
那有人就说了, 这不说的屁话吗?
经过笔者实验, 倒是发现了一些规律. 我们继续按照这个规律往下走.
旋转X轴的时候, 同时看当前Z轴的度数, Z轴为90度的奇数倍, 旋转Y轴, 否则旋转X轴. 旋转Y轴的时候, 同时看当前Z轴的度数, Z轴为90度的奇数倍, 旋转X轴, 否则旋转Z轴. 旋转Z轴的时候, 继续旋转Z轴
这样子我们的旋转方向就搞定了.
if (nextRotateDir[0] == "X") {
if (Math.floor(Math.abs(lastRotate.lastRotateZ) / 90) % 2 == 1) {
lastTransform[`rotateY`] = (lastRotate[`lastRotateY`] + 90 * dir) + 'deg';
} else {
lastTransform[`rotateX`] = (lastRotate[`lastRotateX`] - 90 * dir) + 'deg';
}
}
if (nextRotateDir[0] == "Y") {
if (Math.floor(Math.abs(Math.abs(lastRotate.lastRotateZ)) / 90) % 2 == 1) {
lastTransform[`rotateX`] = (lastRotate[`lastRotateX`] + 90 * dir) + 'deg';
} else {
lastTransform[`rotateZ`] = (lastRotate[`lastRotateZ`] + 90 * dir) + 'deg';
}
}
if (nextRotateDir[0] == "Z") {
lastTransform[`rotate${nextRotateDir[0]}`] = (lastRotate[`lastRotate${nextRotateDir[0]}`] - 90 * dir) + 'deg';
}
然而, 这还没有完, 这种方式的旋转还有个坑, 就是我不知道该旋转90度还是-90度了.
这里并不是简单的上下左右去加减.
旋转方向对了, 旋转角度不知该如何计算了.
具体代码可以查看源码.
彩蛋时间
⚠️⚠️⚠️ 同时这里会伴随着「万向锁」的出现, 即是Z轴与X轴重合了. 哈哈哈哈~
⚠️⚠️⚠️ 这里笔者还没有解决, 也希望万能的网友能够出言帮忙~
⚠️⚠️⚠️ 笔者后续解决了会更新的. 哈哈哈哈, 大坑.
好了, 这里问题不影响我们的项目. 我们继续讲如何找到最短路径并给出提示.
最短路径的计算
在迷宫中, 从一个点到另一个点的最短路径怎么计算呢? 这里笔者使用的是广度优先遍历(BFS)算法来计算最短路径.
我们来思考:
二维数组中找最短路径 每一格的最短路径只有上下左右相邻的四格 那么只要递归寻找每一格的最短距离直至找到终点
这里我们需要使用「队列」先进先出的特点.
我们先来看一张图:
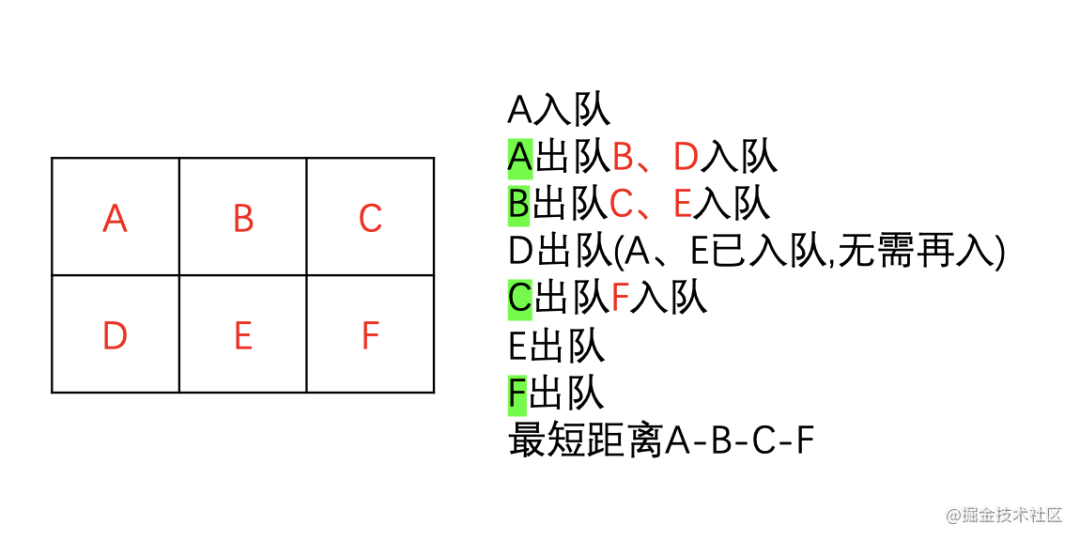
很清晰的可以得到最短路径.
注意
使用两个长度为4的数组表示上下左右相邻的格子需要相加的下标偏移量.
每次入队之前需要判断是否已经入队了.
每次出队时需要判断是否是终点.
需要记录当前入队的目标的父节点, 方便获取到最短路径.
我们来看下代码:
//春初路径
var stack = [];
/**
* BFS 实现寻路
* @param {*} grid
* @param {*} start {x: 0,y: 0}
* @param {*} end {x: 3,y: 3}
*/
function getShortPath(grid, start, end, a) {
let maxL_x = grid.length;
let maxL_y = grid[0].length;
let queue = new Queue();
//最短步数
let step = 0;
//上左下右
let dx = [1, 0, -1, 0];
let dy = [0, 1, 0, -1];
//加入第一个元素
queue.enqueue(start);
//存储一个一样的用来排查是否遍历过
let mem = new Array(maxL_x);
for (let n = 0; n < maxL_x; n++) {
mem[n] = new Array(maxL_y);
mem[n].fill(100);
}
while (!queue.isEmpty()) {
let p = [];
for (let i = queue.size(); i > 0; i--) {
let preTraget = queue.dequeue();
p.push(preTraget);
//找到目标
if (preTraget.x == end.x && preTraget.y == end.y) {
stack.push(p);
return step;
}
//遍历四个相邻格子
for (let j = 0; j < 4; j++) {
let nextX = preTraget.x + dx[j];
let nextY = preTraget.y + dy[j];
if (nextX < maxL_x && nextX >= 0 && nextY < maxL_y && nextY >= 0) {
let nextTraget = { x: nextX, y: nextY };
if (grid[nextX][nextY] == a && a < mem[nextX][nextY]) {
queue.enqueue({ ...nextTraget, f: { x: preTraget.x, y: preTraget.y } });
mem[nextX][nextY] = a;
}
}
}
}
stack.push(p);
step++;
}
}
/* 找出一条最短路径**/
function recall(end) {
let path = [];
let front = { x: end.x, y: end.y };
while (stack.length) {
let item = stack.pop();
for (let i = 0; i < item.length; i++) {
if (!item[i].f) break;
if (item[i].x == front.x && item[i].y == front.y) {
path.push({ x: item[i].x, y: item[i].y });
front.x = item[i].f.x;
front.y = item[i].f.y;
break;
}
}
}
return path;
}
这样子我们就可以找到一条最短路径并得到最短的步数.
然后我们继续去遍历我们的原数组(即棋盘原数组).
点击提示点亮路径.
var step = getShortPath(panArr, { x: 0, y: 0 }, { x: 14, y: 14 }, 0);
console.log("最短距离----", step);
_perstep.innerHTML = `请在${step}步内走到终点`;
var path = recall({ x: 14, y: 14 });
console.log("路径---", path);
/** 提示 */
var tipCount = 0;
_tip.addEventListener("click", () => {
console.log("9999", tipCount)
elArr.forEach((item, index) => {
let r = Math.floor(index / 15);
let c = index % 15;
path.forEach((_item, i) => {
if (_item.x == r && _item.y == c) {
// console.log("ooo",_item)
if (tipCount % 2 == 0)
item.classList = "pan-item pan-path";
else
item.classList = "pan-item";
}
})
});
tipCount++;
});
这样子, 我们可以得到如图的提示:
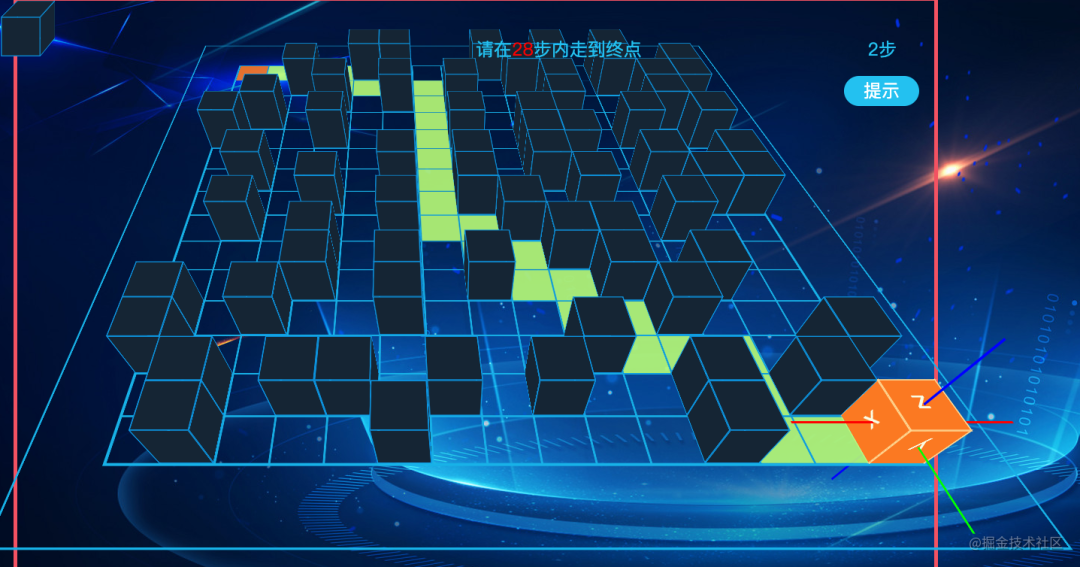
大功告成. 嘿嘿, 是不是很惊艳的感觉~
尾声
当然, 我这里的这个小游戏还有可以完善的地方 比如:
可以增加道具, 拾取可以减少已走步数 可以增加配置关卡 还可以增加跳跃功能 ...
原来如此, CSS3D能做的事还有很多, 怎么用全看自己的想象力有多丰富了.
哈哈哈, 真想用CSS3D写一个「我的世界」玩玩, 性能问题恐怕会有点大.
本文例子均在PC端体验较好.
试玩地址
https://xdq1553.github.io/-CSS3D-/
源码地址
https://github.com/xdq1553/-CSS3D-
作者:起小就些熊
https://juejin.cn/post/7000963575573381134
- EOF -
1、奇技淫巧 :巧用 CSS sticky 实现返回顶部功能
2、只需一行 CSS 代码,让长列表网页的渲染性能提升几倍以上!
3、十几个 CSS 高级常见技巧汇总:虚线框、三角形等
关注「程序员的那些事」加星标,不错过圈内事
点赞和在看就是最大的支持❤️